3 数学归纳法

3.1 数学归纳法

3.1.1 引入

在这一讲当中，我们会介绍一种叫做 数学归纳法(mathematical induction) 的证明技巧。归纳是一种非常强大的工具，它能够建立一个关于所有自然数都成立的语句。当然，自然数有无穷多个，但归纳提供了一种通过有限的步骤去证明无穷的结论的方法。

让我们通过一个例子来直观地阐释一下归纳背后的基本思想。假设我们想要证明下面的命题：

$\forall n\in\mathbb{N}, \sum_{i=0}^{n}i = \frac{n(n+1)}2\tag{1}$

你会怎么证明这个式子呢？可能你会先尝试代入 $n = 0, 1, 2$ 验证一下成立，并以此类推。但是，需要代入验证的 $n$ 的取值有无穷多个。此外，检查前几个 $n$ 的值成立并不足以得出这句话对于所有的 $n\in\mathbb{N}$ 都成立的结论，就像下面的例子所展现的那样：

概念检查

考虑命题：“ $\forall n\in\mathbb{N}, n^2 - n + 41$ 是一个质数”。尝试验证这句话对于前面一些自然数是对的。（事实上，你可以一直检查到 $n = 40$ 也不能找到一个反例！） 现在，检查一下 $n = 41$ 的情况。

在数学归纳法中，我们通过一个有趣的观察来规避这个问题：假设这个命题对于某个 $n = k$ 是成立的，即 $\sum_{i=0}^{k}i = \frac{k(k+1)}2$。（这称为 归纳假设(induction hypothesis) ）那么：

$\sum_{i=0}^{k}i + (k+1) = \frac{k(k+1)}2 + (k+1) = \frac{(k+1)(k+2)}2\tag{2}$

也就是说，原命题对于 $n = k + 1$ 也成立！换句话说，如果这句话对于 $n = k$ 成立，那么它一定对于 $n = k + 1$ 也成立。上述的论证称为 归纳步骤(inductive step) 。

归纳步骤是一个非常强大的工具：如果我们可以说明，如果一个语句对于某个 $k$ 成立，根据归纳步骤，我们就可以得到这个语句对于 $k + 1$ 也成立的结论；有了 $k + 1$ 的情况之后，根据归纳步骤，我们又可以继续得到 $k + 2$ 的情况也成立，以此类推。

事实上，我们可以将上述论证对于所有的 $n\ge k$ 重复无数次。所以呢？我们就能证明等式(1)了吗？快了！

现在的问题是，为了应用归纳步骤，我们必须先确认等式(1)对于某个初始值 $k$ 是成立的。由于我们的目标是证明(1)对于所有的自然数都成立，最显然的选择自然是 $k = 0$。我们称这个 $k$ 的选择为 基础情况(base case) 。然后，如果基础情况成立，那么数学归纳法的公理告诉我们：归纳步骤能够保证等式(1)对于所有的 $n\in\mathbb{N}$ 都成立。

定理3.1

$\forall n\in\mathbb{N},\sum_{i=0}^{n}i=\frac{n(n+1)}2$

定理3.1证明

证明：对变量 $n$ 进行归纳。

基础情况( $n=0$ )：这里，我们有 $\sum_{i=0}^{0}i = 0 = \frac{0(0+1)}2$。于是，基础情况成立。

归纳假设：对于某个任意的 $n = k \ge 0$ ，假设 $\sum_{i=0}^{k}i=\frac{k(k+1)}2$。

用语言表述，归纳假设就是在说“让我们假装我们已经证明了原命题对于某个任意的 $n = k \ge 0$ 成立了”。

归纳步骤：证明原命题对于 $n = k + 1$ 成立，即说明 $\sum_{i=0}^{k+1} i = \frac{(k+1)(k+2)}2$ ：

$\sum_{i=0}^{k+1}i = \sum_{i=0}^{k} i + (k+1) = \frac{k(k+1)}2 + (k+1) = \frac{(k+1)(k+2)}2\tag{3}$

其中，第二个等号是根据归纳假设得出的。

根据数学归纳法的原理，原命题成立。 $\square$

概念检查

在等式(3)中，归纳假设到底是如何帮助我们得到第二个等号的呢？(提示：我们用它将 $\sum_{i=0}^{k}i$ 替换成了一些很有用的东西)

3.1.2 归纳

我们到目前为止学了些什么呢？用 $P(n)$ 表示命题 $\sum_{i=0}^{n}i = \frac{n(n+1)}2$ ，我们的目标是证明 $\forall n\in\mathbb{N}, P(n)$ 。 归纳原则(principle of induction) 断言证明这个需要三个简单的步骤：

1. 基础情况(Base Case) ：证明 $P(0)$ 为真；
2. 归纳假设(Induction Hypothesis) ：对于某个任意的 $k\ge 0$ ，假设 $P(k)$ 是真的；
3. 归纳步骤(Inductive Step) ：基于归纳假设，证明 $P(k+1)$ 也是真的。

让我们用*多米诺骨牌(dominoes)*的方式将这三个步骤可视化出来。用一排依次标记上 $0,1,2,...,n$ 的多米诺骨牌表示语句 $P(i)$ ，其中 $P(0)$ 和第0个骨牌相对应， $P(1)$ 和第1个骨牌相对应，以此类推。

由于多米诺骨牌靠近着排成了一排，如果我们向后撞倒了第k个骨牌，它就会推倒第k+1个骨牌。推倒了第k个骨牌就相当于证明了 $P(k)$ 为真。 递归步骤就相当于证明了骨牌之间的距离足以让上一个骨牌被撞倒的时候撞倒下一个骨牌。

基础情况 （ $n=0$ ） 推倒了第0个骨牌，从而引发了一个连锁反应，推倒了所有的骨牌，相当于证明了所有的 $P(i)$ 。

最后，关于选择一个合适的基础情况再说一点。在上面的例子中我们选择了 $k = 0$ ，但是，一般的基础情况的选取是取决于你想要证明的主张的，并不是任何时候都选 $k = 0$ 。

3.1.3 实例

费马小定理

下面我们再做一个归纳法证明的例子。先回忆一下第一讲当中的一个定义，对于整数 $a, b$ ，我们称 $a$ 整除 $b$ ，记作 $a | b$ ，当且仅当存在整数 $q$ 满足 $b = aq$ 。

定理3.2

$\forall n\in\mathbb{N}, 3 | (n^3 - n)$

定理3.2证明

证明：对 $n$ 进行归纳。用 $P(n)$ 表示 $3 | (n^3-n)$。

基础情况( $n = 0$ )：$P(0)$ 表示 $3 | 0^3 - 0$ ，即 $3 | 0$ ，显然正确，因为任何非零整数都整除0。

归纳假设：假设对于某个任意 $n = k \ge 0$ ， $P(k)$ 是真的。也就是说 $3 | k^3 - k $ 。

归纳步骤：下面我们说明 $P(k+1)$ 是真的，即 $3 | ((k+1)^3 -(k+1))$ 。为了证明这个结论，我们对 $(k + 1)^3 - (k + 1)$ 作如下展开： $$ (k + 1)^3 - (k + 1) = k^3 - k + 3k(k+1) $$

而 $3 | k^3 - k \wedge 3 | 3k(k+1)$ ，所以 $3 | (k + 1)^3 - (k + 1)$ 。（定理2.1）

由归纳原则， $\forall n\in\mathbb{N}, 3|(n^3-n)$ 。 $\square$

概念检查

在上面的例子中，归纳假设是如何帮助我们证成归纳步骤的呢？

双色定理

我们现在开始看一个更进一步的归纳法的例子，这个例子是著名的*四色定理(four color theorem)*的简化版本。四色定理是说任何的地图都可以用四种颜色染色，使得任意两个相邻的国家不同色。

这里，相邻国家的定义是两个国家有公共的，不简单的边界，眼下之意就是需要有公共边，只有一个公共点不算相邻。

四色定理的证明十分困难，从1852年这个定理被第一次提出以来，有过一些最终被证明是伪证的证明。事实上，直到1976年，一个借助了计算机帮助的定理证明 (opens new window)才被Appel和Haken给出。

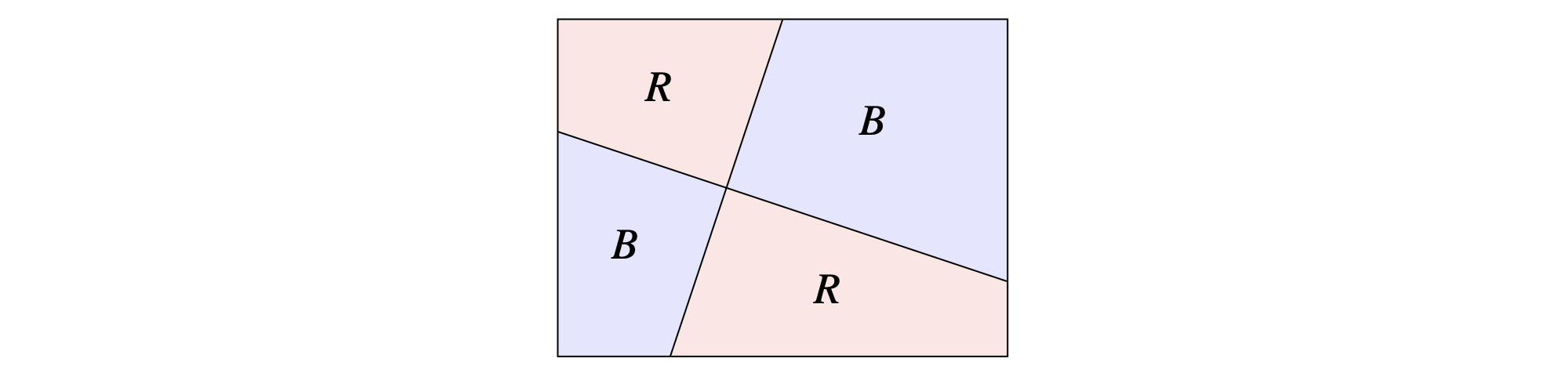
在这一讲中，我们考虑一个更简单版本的四色定理。我们定义地图以在长方形中画直线的方式给出，每条直线会将长方形分成两个区域。我们能够用不超过两种颜色（比如说红色和蓝色）为这个简化版的地图染色，使得任意两个相邻的区域不同色吗？为了表意更清楚一些，这里是一个2-染色的地图示例：

定理3.3

令 $P(n)$ 表示语句“任意一张上述形式的有n条线的地图是可二染色的”，有 $\forall n\in\mathbb{N} P(n)$ 。

这里 可二染色的(two-colorable) 的含义是 最多 用两种颜色可以将图染色且相邻的部分不同色。

定理3.3证明

证明：对 $n$ 进行归纳。

基本情况( $n=0$ )： $P(0)$ 显然成立，由于我们有0条线，整个地图只有1个区域，我们只需用一种颜色染整个地图即可实现二染色。

归纳假设：对于某个任意的 $n = k \ge 0$ ，假设 $P(k)$ 。

归纳步骤：下面，我们证明 $P(k + 1)$ 。我们有一张 $k + 1$ 根线的地图并且希望说明它可以二染色。考虑移除其中的某一条线，图上现在只有 $k$ 条线，归纳假设告诉我们，此时的地图是可以二染色的。

观察到一个事实，给定一种合理的染色方案，我们将所有的红色变成蓝色，蓝色变成红色，得到的新的染色方案依旧是合理的。

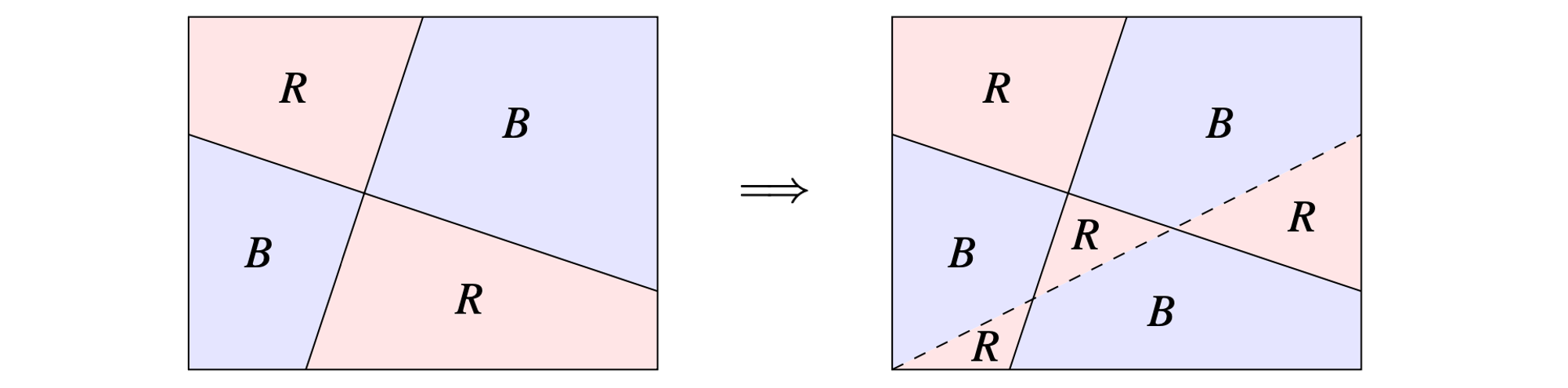
考虑上述事实，我们将之前移除的那条线再放回去，让线的一侧的所有区域颜色保持不变，线的另一侧的所有区域颜色翻转，如下图所示：

于是，我们得到了 $k + 1$ 根线的地图上的一个有效的二染色方案，即 $P(k + 1)$ 为真。

为什么这个二染色方案是有效的呢？考虑共享一个边界的任意两个相邻的区域，下面两种情况必有一种情况成立：

• 公共边是我们刚刚移除然后又放回去的那条线，即第 $k + 1$ 条线。
  • 根据前面的构造过程，这条线虽然一开始两边的颜色是相同的，但我们将这条线的一侧颜色全部翻转了，因此现在的这两个区域颜色肯定不同；
• 公共边是前 $k$ 条线里面的某一条。
  • 由归纳假设以及前面关于翻转颜色的一个基本事实可知，两个区域的颜色肯定也不一样。

综上，我们给出的方案是一个有效的二染色方案，即 $P(k+1)$ 为真。

由归纳原理可得，原命题为真。 $\square$

3.2 强化归纳假设

3.2.1 引入

在使用归纳法的时候，选择正确的语句来证明是很重要的。比如说，假设我们希望证明“ $\forall n\ge 1$ ，前 $n$ 个奇数的和是一个完全平方数”。下面是一个归纳法的证明尝试：

尝试证明：我们对 $n$ 进行归纳。

基础情况(n = 1)：第一个奇数是 $1$ ，是一个完全平方数。

归纳假设：假设前 $k$ 个奇数的和是完全平方数，比如说 $m^2$ 。

归纳步骤：第 $k + 1$ 个奇数是 $2k+1$ 。于是，根据归纳假设，前 $k + 1$ 个奇数的和为 $m^2 + 2k + 1$。但这个时候我们卡住了。为什么 $m^2 + 2k + 1$ 是一个完全平方数呢？

似乎，我们的归纳假设太“弱”了，它并没有给我们足够的结构来说明任何对于 $k+1$ 的情形有用的东西。

让我们暂时后退一步，并且做一些基本的检查来确认一下我们的主张并不是显然错的。先计算前面几个 $n$ 的情况，说不定在这个过程当中，我们会发现一些被忽略的隐藏的结构：

• $n = 1$ ： $1 = 1^2$ 是完全平方数。
• $n = 2$ ： $1 + 3 = 4 = 2^2$ 是完全平方数。
• $n = 3$ ： $1 + 3 + 5 = 9 = 3^2$ 是完全平方数。
• $n = 4$ ： $1 + 3 + 5 + 7 = 16 = 4^2$ 是完全平方数。

看起来我们有了一个好消息和一个更好的消息。好消息是，试了几次，我们并没有找到反例。更好的消息是，我们发现了一个令人振奋的规律：前 $n$ 个奇数的和不仅是一个完全平方是，并且恰好等于 $n^2$ ！在这个发现的激励下，让我们尝试一些不那么直观的东西；去证明下面这个*更强(stronger)*的主张。

定理3.4

对于任意的 $n \ge 1$ ，前 $n$ 个奇数的和为 $n^2$ 。

定理3.4证明

证明：对 $n$ 进行归纳。

基础情况( $n = 1$ )：第1个奇数是 $1$ ，等于 $1^2$ 。

归纳假设：假设前 $k$ 个奇数的和是 $k^2$。

归纳步骤：第 $k + 1$ 个奇数为 $2k+1$ ， 由归纳假设，前 $k$ 个奇数的和为 $k^2$ ，于是前 $k + 1$ 个奇数的和为 $k^2 + 2k + 1 = (k + 1)^2$ 。

综上，根据归纳原理，原命题成立。 $\square$

3.2.2 归纳

说直白点，我们无法证明原来的命题，所以，我们假设了一个更强的命题并设法证明了它。这到底为什么能起作用呢？原因是我们原来的命题并没有捕捉到我们想要证明的底层事实的真正的 结构(structure) ——它太模糊了。因此，我们的归纳假设不够强大，不足以完成归纳步骤。

相比之下，我们的第二个主张会强一些，并且更重要的是它里面有更多的明确的结构，这使得我们的归纳假设更加强烈——我们不仅可以使用前 $k$ 个奇数的和是完全平方数这个条件，我们还可以使用和等于 $k^2$ 这个条件。这个额外的结构恰好是我们完成这个证明所需要的。

总结一下，通过上面的例子，我们说明了尽管一个命题是真的，更加准确的，不模糊的归纳假设更有利于归纳步骤的进行，更容易写出一个成功的归纳证明。

3.2.3 实例

让我们再来尝试一个例子。假设我们想要证明一个主张：“对于所有的 $n\ge 1$ ，有 $\sum_{i=1}^{n}\frac1{i^2} \le 2$ ”。

概念检查

一个“显然”的归纳假设是这样的：假设对于 $n = k$ ， $\sum_{i=1}^{k}\frac1{i^2} \le 2$ 。为什么这不足以证明对于 $n = k + 1$， $\sum_{i=1}^{k}\frac1{i^2} + \frac1{(k+1)^2} \le 2$ ？（提示： $\sum_{i=1}^k\frac1{i^2}$ 有可能真的等于2吗？）

现在，让我们做一些反直觉的事情——证明下面一个更强的命题，也就是强化我们的归纳假设。

定理3.5

$\forall n\ge 1, \sum_{i=1}^n\frac1{i^2}\le 2-\frac1n$

定理3.5证明

证明：对 $n$ 进行归纳。

基础情况（ $n = 1$ ）：我们有 $\sum_{i=1}^1\frac1{i^2}=1 \le 2 - \frac11$ 成立。

归纳假设：假设原命题对于 $n = k$ 成立。

归纳步骤：根据归纳假设，我们有

$\sum_{i=1}^{k+1}\frac1{i^2} = \sum_{i=1}^{k}\frac1{i^2} + \frac1{(k+1)^2} \le 2 - \frac1k + \frac1{(k+1)^2}$

$= 2 - \frac1{k+1} - \frac1{k(k+1)^2} \le 2 - \frac1{k+1}$

练习：自己尝试一下上述归纳步骤中的推导。

根据归纳原则，原命题成立。 $\square$

3.3 简单归纳法与强归纳法

3.3.1 概念

到现在为止我们已经学习的数学归纳法也叫做 简单(simple) 归纳或者 弱(weak) 归纳。还有一种我们接下来将要讨论的归纳方法，称为 强归纳法(strong induction) 。强归纳法和简单归纳法整体是类似的，唯一的区别是两者的归纳假设不同：

• 简单归纳法假设 $P(k)$ 为真，就像我们先前一直做的那样；

• 强归纳法假设一个更强的语句：$P(0), P(1), ..., P(k)$ 都是真的，即

  $\bigwedge_{i=0}^{k}P(i)\ is\ true$

那么强归纳和若归纳在证明能力上有区别吗？换句话说，强归纳法可以证明用简单归纳法无法证明的语句吗？不可以！

直观地，这一点可以从我们最开始的多米诺骨牌的类比当中看出。在这个情景中，

• 弱归纳是在说如果第k个骨牌倒了，第k+1个骨牌也会倒；
• 强归纳是在说如果第0个到第k个骨牌都倒了，那么第k+1个骨牌也会倒。

但这两种情况其实是等价的：如果第0个骨牌倒了，重复的使用简单归纳，我们就能够得到第0个骨牌会把前面k个都压倒，到第k+1个，恰好就是强归纳法的情况。

因此，强归纳法和若归纳法在证明能力上面是等价的。

但是，强归纳法有一个吸引人的优点——它可以让证明的书写过程更容易一些，因为我们可以使用一个更强的归纳假设。我们怎么理解这两者的关系呢？考虑一个螺丝刀和一个电动螺丝刀，它们都能将螺丝拧下来，完成了相同的任务，但是显然电动螺丝刀使用起来会更容易些。

3.3.2 实例

下面我们来看一个强归纳法的简单例子。此外，这是我们的第一个需要多个基础情况的归纳证明。

定理3.6

$\forall n\in\mathbb{N}\wedge n\ge 12,\exists x,y\in\mathbb{N}, n=4x+5y$

定理3.6证明

证明：对 $n$ 进行归纳。

基础情况（ $n = 12$ ）：我们有 $12 = 4 \cdot 3 + 5 \cdot 0$ 。

基础情况（ $n = 13$ ）：我们有 $13 = 4 \cdot 2 + 5 \cdot 1$ 。

基础情况（ $n = 14$ ）：我们有 $14 = 4 \cdot 1 + 5 \cdot 2$ 。

基础情况（ $n = 15$ ）：我们有 $15 = 4 \cdot 0 + 5 \cdot 3$ 。

归纳假设：假设原命题对于所有的 $12\le n\le k$ 成立，其中 $k\ge 15$。

归纳步骤：下面证明 $n = k + 1 \ge 16$ 时结论成立。特别地，$(k + 1) - 4 \ge 12$ ， 由归纳假设，有

$\exists x',y'\in\mathbb{N}, (k+1)-4 = 4x' + 5y'$

令 $x = x' + 1, y = y'$，则

$k + 1 = 4x' + 5y' + 4 = 4(x'+1) + 5y' = 4x+5y$

根据归纳原则，原命题成立。 $\square$

概念检查

如果我们选择若归纳法而不是强归纳法，为什么我们证不出来？

下面我们来看一个更高级一点的例子。为了这个例子，请回忆一下我们之前提过如果一个自然数 $n$ 是质数意味着它只有 $1$ 和 $n$ 两个因数。

定理3.7

任意自然数 $n > 1$ 可以写成一个或者多个质数的乘积。

定理3.7证明

证明：对 $n$ 进行归纳。用 $P(n)$ 表示 “ $n$ 可以写成一个或者多个质数的乘积”。

基础情况(n = 2)：因为2是质数，$P(2)$ 显然成立。

归纳假设：对于 $2 \le n \le k$ ， $P(n)$ 成立。

归纳步骤：下面证明 $P(k+1)$ 成立。分两种情况，

• $k + 1$ 为质数，则 $P(k+1)$ 显然成立。
• $k + 1$ 不是质数，则 $\exists x,y\in\mathbb{N}, 2 \le x,y \le k, k + 1 = xy$，由归纳假设有 $P(x)\wedge P(y)$ ，而 $k + 1 = xy$ ，于是 $P(k+1)$ 成立。

综上，由归纳原理，原命题成立。 $\square$

概念检查

如果我们使用简单归纳，为什么会证明失败？（提示：假设 $k + 1 = 42$ ，由于 $42 = 6 \times 7$ ，也就是说在归纳步骤当中我们希望使用 $P(6)$ 与 $P(7)$ ，但是弱归纳的归纳假设并不能给我们这个条件 ——那么弱归纳法能够给我们的条件是什么呢？）

3.3.3 理解

最后，我们来形式化地谈谈强归纳法和弱归纳法为什么等价这个问题。考虑 $Q(n) = P(0)\wedge P(1) \wedge ... \wedge P(n)$ ，其实对 $P$ 强归纳就相当于是对 $Q$ 弱归纳。试着理解一下。

3.4 递归、编程与归纳法

在归纳和递归之间有着非常紧密的联系，我们下面会通过两个例子来探索一下这种联系。

3.4.1 斐波那契的兔子

13世纪有一位非常著名的意大利数学家斐波那契，他在1202年思考了下面的这个谜题：从一对兔子开始，如果每对兔子从第二个月开始的每个月都能生下一对新兔子（言下之意就是这对兔子刚刚出生的那个月是没有生育能力的），那么一年之后会有多少对兔子呢？这个人口数量增长的模型可以通过递归地定义一个函数来刻画，它的结果数列现在被称为 斐波那契数列(Fibonacci numbers) 。

为了能够递归地模拟兔子人口的增长，用 $F(n)$ 表示第 $n$ 个月兔子的兔子数量。根据上述规则，我们的初始情况为：

• 显然 $F(0) = 0$；
• 在第一个月，我们手动引入了第一对新生的兔子，意味着 $F(1) = 1$；
• 由于新生的兔子要经过一个月之后才能有生育能力，因此第二个月依然只有一对兔子，即 $F(2) = 1$；

从第三个月开始，有趣的事情发生了。比如 $F(3) = 2$ ，由于原本的那一对兔子有生育能力了，这个月它们会生下新的一对兔子。那么，对于一个一般的值 $n$ , $F(n)$ 如何呢？貌似直接给出 $F(n)$ 的一个显式的公式是很困难的。然而，我们可以像下面这样 递归地(recursively) 定义 $F(n)$ 。

• 在第 $n - 1$ 个月，根据定义，我们有 $F(n-1)$ 对兔子。那么，这些兔子中有多少室友生育能力的呢？
• 只有在第 $n - 2$ 个月就已经出生的兔子在第 $n-1$ 个月才有生育能力，也就是说在 $F(n - 1)$ 对兔子中只有 $F(n - 2)$ 对是具有生育能力的。
• 于是，从第 $n - 1$ 个月到第 $n$ 个月的过程中，出生了 $F(n - 1)$ 对兔子，从而第 $n$ 个月的时候，总共有 $F(n) = F(n - 1) + F(n - 2)$ 只兔子。

总结一下：

• $F(0) = 0$ ；
• $F(1) = 1$ ；
• 对于 $n \ge 2$ ， $F(n) = F(n - 1) + F(n - 2)$ 。

非常简洁，不过你可能会疑惑我们一开始为什么会关心兔子的繁殖问题。其实这个简化的人口增长模型揭示了一个原理：在不加约束的情况下，人口会随着时间以指数级的速度增长。下面的这个练习给出了这种指数级增长的一个下界。（真正的增长率会更大一下，大约在 $1.6^n$ 这个量级）

练习

使用归纳法证明斐波那契数满足 $\forall n\ge 3, F(n)\ge 2^{(n-1)/2}$。注意你将会需要两个基本情况：$n = 3$ 和 $n = 4$ （为什么？）

实际上，理解这个不加限制情况下的指数级人口增长是导致达尔文构建他的 进化论(theory of evolution) 的关键一步。引用一下达尔文的一句话：

There is no exception to the rule that every organic being increases at so high a rate, that if not destroyed, thet earth would soon be covered by the progeny of a single pair. —— Darwin

我们在标题里面说过这个小节需要编程，到了兑现承诺的时候了——一个简单的计算 $F(n)$ 的递归程序：

练习

这个程序计算 $F(n)$ 需要花多久？或者说，我们需要调用 $F(n)$ 这个函数多少次？ 你应当能够通过归纳的方式得出至少 $F(n)$ 需要调用多少次它自己。（提示：找递推关系，然后放缩，结果是指数级）

上面的这个练习应当能够让给你觉得善变的方法是一个非常低效的计算第 $n$ 个斐波那契数的方法。这里有一个快得多的迭代算法能够完成相同的任务（这是应该是一个很熟悉的将 尾递归(tail-recursion) 转化成迭代算法的例子）：

练习

这个迭代算法要花多长时间完成 $F_2(n)$ 的计算呢？换句话说，这个循环经过了多少次迭代才能终止呢？你可以通过归纳法来证明 $F_2(n) = F(n)$ 吗？

3.4.2 二分查找

我们下面使用归纳法来分析一个你的奶奶可能很熟悉的一个递归的算法——二分查找！我们会查字典的语境下讨论二分查找：为了找到单词 $W$ ，我们从 中间打开字典。

• 如果这一页的第一个单词在 $W$ 的后面，我们就在字典的前一半（中间页前面的那些页）中继续类似地查找；
• 否则，我们就在字典的后一半（从中间页往后）中继续做类似的查找。
  • （如果字典是偶数页，比如说 $2m$ 页，我们定义第 $m + 1$ 页为中间页）
• 一旦我们将查找的范围缩小到一页的时候，我们会在这一页上诉诸于一种暴力的挨个比对的方式来在这一页中查找单词 $W$ 。

上述算法用伪代码描述为如下：

让我们用归纳法来证明一下FindWord的正确性，也就是说如果 $W$ 在字典 $D$ 中，它能够返回 $W$ 的定义。这个证明需要我们使用强归纳法，而不是弱归纳法。

算法3.1正确性证明

证明：我们对字典 $D$ 的页数 $n$ 进行归纳。

基础情况（ $n = 1$ ）：如果 $D$ 只有一页，那么第4行会暴力搜索 $W$ 。于是，如果 $W$ 存在，就会被找到并返回；如果不存在，则会返回 “W not found”。这就是我们期待的结果。

归纳假设：假设对于 $1\le n\le k$ ，FindWord 结果都正确。

归纳步骤：我们下面来证明 FindWord 对于 $n = k + 1$ 也正确。

在第8行之后，我们知道了一个新的单词 $W'$ ；于是我们就可以确定 $W$ 一定在 $D$ 的前一半或者后一半中。第一种情况下，根据第10行，我们在 $D$ 的前一半中递归；第二种情况下，根据第12行，我们在 $D$ 的后一半中递归。

由归纳假设，递归调用能够正确的在前一半或者后一半字典中正确的找到 $W$ 或者返回 “W not found”，因为一半字典最多不超过 $k$ 页。

而我们返回的是递归调用的值，因此 FindWord 能够正确的在有 $k + 1$ 页的字典 $D$ 中查找单词 $W$ 。

综上，根据归纳原理，FindWord 是正确的。 $\square$

概念检查

为什么在上面的证明中，我们需要使用强归纳法呢？

3.5 伪证

如果你的证明过程是错的，那么你很可能会证明出一个错误的结论。在上世纪中叶，有一个常用的口头表达：“那是一匹颜色不同的马”，常常用来指代一些不同寻常的事情。著名的数学家乔治·波利亚，也是一个伟大的为非专业人士解释数学的学者，给出了下面的证明来展示不存在不同颜色的马。

定理3.8

所有的马颜色都相同。

定理3.8证明

证明：对马的数量 $n$ 进行归纳。用 $P(n)$ 表示我们想证明的主张。

基础情况(n = 1)：$P(1)$ 显然正确，因为如果集合中只有一匹马，那么集合中所有的马的颜色肯定相同。

归纳假设：对于某个任意的 $n\ge 1$ ， $P(n)$ 成立。

归纳步骤：给定一个有 $n + 1$ 只马的集合 $\{h_1, h_2, ..., h_n+1\}$ ，我们可以排除第 $n + 1$ 只马，对前 $n$ 只马 $\{h_1, h_2, ..., h_n\}$ 应用归纳假设，推导出它们具有相同的颜色。同理，我们也可以推导出 $\{h_2, h_3, ..., h_{n+1}\}$ 也具有相同的颜色。由于“中间”的马 $\{h_2, h_3, ..., h_n\}$ 同时属于上述的两个集合，所以他们和 $h_1$ 以及 $h_{n+1}$ 的颜色相同。 从而，这 $n + 1$ 只马都具有相同的颜色。

综上，由归纳原理，原命题成立。 $\square$

显然，所有的马具有相同的颜色是不对的。所以，我们到底哪儿错了呢？回忆一下，为了能够应用归纳原则，在归纳步骤中，我们必须证明 $\forall n\ge 1, P(n)\Longrightarrow P(n+1)$ 。而在上面的那个证明过程中，这一步是错的——特别的，存在一个 $n$ 产生了反例。

练习

对于哪个 $n$ 来说， $P(n)\Longrightarrow P(n+1)$ 是假的呢？（提示：考虑在证明中所提到的“中间”的马的关键性质。）

3.6 练习题

3.6.1 平方序列的和

求证：$\forall n\in\mathbb{N}, 0^2 + 1^2 + 2^2 + 3^2 + ... + n^2 = \frac16n(n+1)(2n+1)$ 。

解答

证明：对 $n$ 进行归纳。

基础情况（ $n = 0$ ）：前0项的和为 $0^2 = 0 = \frac16\cdot 0\cdot(0+1)\cdot(2\cdot 0+1)$ 成立。

归纳假设：假设对于 $n = k \ge 0$ 时，结论成立。

归纳步骤：下面证明 $n = k + 1$ 时，结论成立。

$\sum_{i=0}^{k+1}i^2 = \sum_{i=0}^{k}i^2 + (k+1)^2 = \frac16k(k+1)(2k+1) + (k+1)^2$

$=\frac16(k+1)(k(2k+1) + 6(k+1))= \frac16(k+1)(k+2)(2k+3)$

综上，根据归纳原则，原命题成立。

3.6.2 伯努利不等式

在实际分析中， 伯努利不等式(Bernoulli's Ine) 是一个用于逼近 $(1+x)$ 的指数的不等式。求证这个不等式：

$n\in\mathbb{N}\wedge 1+x>0\Longrightarrow (1+x)^n\ge 1+nx$

解答

证明：对 $n$ 进行归纳。

基础情况（ $n = 0$ ）： $(1 +x)^0 \ge 1 + 0\cdot x$ 显然成立。

归纳假设：假设 $n = k$ 时， $(1+x)^k\ge 1+kx$。

归纳步骤：$n = k + 1$ 时，有

$(1+x)^{k+1} = (1+x)^k(1+x) \ge (1+kx)(1+x)$

$= 1+(k+1)x + kx^2 \ge 1 + (k+1)x$

综上，根据归纳假设，原命题成立。 $\square$

3.6.3 阶乘

一个常见的递归定义的函数是阶乘(factorial)，对于一个非负整数 $n$ ，定义 $n! = n(n-1)(n-2)...1$ ，基础情况为 $0! = 1$ 。下面让我们通过证明一个关于阶乘的不等式来强化一下我们对于归纳法和递归之间联系的理解。

$\forall n\in\mathbb{N}, n > 1 \Longrightarrow n! < n^n$

使用数学归纳法证明上述命题。（提示：在归纳步骤中，将 $(n+1)!$ 写成 $(n+1)\cdot n!$ 并使用归纳假设。）

解答

证明：对 $n$ 进行归纳。

基础情况（ $n = 2$ ）： $2! = 2 < 4 = 2^2$ 显然成立。

归纳假设：假设 $n = k$ 时， $k! < k^k$ 。

归纳步骤：当 $n = k + 1$ 时，

$(k+1)! = (k+1)\cdot k! < (k+1)\cdot k^k < (k+1)\cdot (k+1) ^ k = (k+1)^{k+1}$

综上，根据归纳原则，原命题成立。 $\square$

3.6.4 名人问题

聚会上的 名人(celebrity) 指的是其他所有人都认识TA但TA不认识任何人的人。假设你在一个有 $n$ 人的聚会上。对于聚会上的任意两个人 $A$ 和 $B$ ，你可以问 $A$ TA是否认识 $B$ 并得到一个诚实回答。给出一个递归的算法，通过问最多 $3n-4$ 个问题，判断聚会上是否存在一个名人，并且如果有的话是谁。

注意：为了解决这个问题，你所能做的操作只是问聚会上的人问题。你所要得到的结果就是是否有名人参加聚会。

用归纳法证明你的算法总是能正确的识别一个名人，如果聚会上有的话。并且你的算法最多只会问 $3n-4$ 个问题。

解答

设计算法：

证明：

首先证明一个引理：聚会上最多只有1个名人。 反证法，假设有2个名人 $i$ 和 $j$。 $i$ 是名人可知 $i$ 不认识 $j$ ，由 $j$ 是名人说明 $i$ 认识 $j$ ，矛盾，引理证毕。

下面证明递归部分 FindPotentialCelebrity(n) 能够返回唯一有可能是名人的人，且只使用 $n - 1$ 个问题。

对 $n$ 进行归纳。

基础情况（ $n = 2$ ）：根据算法第7到10行，我们只问了1个问题 —— 1是否认识2： - 如果1认识2，那么1一定不是名人，返回有可能是名人的2； - 如果1不认识2，那么2一定不是名人，返回有可能是名人的1； 所以，基础情况成立。

归纳假设：假设 FindPotentialCelebrity(k - 1) ( $k\ge3$ )返回前 $k - 1$ 个人中唯一可能是名人的人，且只使用了 $k - 2$ 个问题。

归纳步骤：下面证明 FindPotentialCelebrity(k) 的正确性。 在算法第11行以及归纳假设，我们正确选取了前 $k - 1$ 个人中唯一有可能是名人的人 $p$ ，花了 $k - 2$ 个问题。 在算法第12到15行，问了一个问题：$p$ 是否认识 $k$。

• 如果 $p$ 认识 $k$ ，那么 $p$ 一定不是名人，返回 $k$ ；
• 如果 $p$ 不认识 $k$ ，那么 $k$ 一定不是名人，返回 $p$ 。 因此，FindPotentialCelebrity(k) 成功返回了前 $k$ 个人中唯一可能是名人的人，并且只问了 $k - 2 + 1 = k - 1$ 个问题。

综上，根据归纳原理，FindPotentialCelebrity(n) 成功用 $n - 1$ 次比较找到了 $n$ 个人中唯一有可能是名人的那个人 $p$ 。

之后，算法的第22到33行的检查确保了 $p$ 不认识其他 $n - 1$ 个人中的任何一个并且其他 $n - 1$ 个人都认识 $p$ 。这原本应该是最多需要 $2n-2$ 次比较的，但是由于在计算 FindPotentialCelebrity(n) 的时候已经问过了一个问题，所以这个问题我们就不用再重复问了，因此确认 $p$ 是否真的是名人的步骤最多只需要 $2n - 3$ 次询问。

再加上前面寻找潜在名人的 $n - 1$ 次询问，我们一共最多只需要 $n - 1 + 2n-3 = 3n-4$ 次询问。（最多是因为如果我们在检查的时候发现了 $p$ 不是名人，那么算法会直接返回不存在，后续的检查不会执行，也就不会问更多的问题了）

综上所述，我们的算法能够正确找到聚会上的名人或者告诉我们聚会上没有名人，并且最多只需要问 $3n-4$ 个问题。 $\square$

3.6.5 邮票兑换

借助定理3.6的证明来设计一个算法，给定任意的至少12分的面值，输出可以凑成这个面值的4分和5分邮票的数量。你的算法最多会使用多少张5分的邮票呢？

解答

设计算法：

考虑合成 $n$ 的时候我们的算法需要的5分邮票张数为 $f(n)$ ，由算法第12到14行可知 $f(n) = f(n - 4)$ ，于是我们有

$f(n) = \begin{cases} 0, n \equiv 0 \mod 4 \\ 1, n \equiv 1 \mod 4 \\ 2, n \equiv 2 \mod 4 \\ 3, n \equiv 3 \mod 4 \end{cases}, n\ge 12$

显然，$f(n)_{max} = 3$ ，即我们的算法最多会使用 $3$ 张5分邮票。 $\square$

3.6.6 强化归纳

用数学归纳法证明：

$\forall n\in\mathbb{N}^{*}, \sum_{i=1}^{n} \frac1{i^3} \le 2$

其中，$\mathbb{N}^{*}$表示正整数。

解答

证明：我们证明一个更强的命题：

$\forall n\in\mathbb{N}^{*}, \sum_{i=1}^{n} \frac1{i^3} \le 2 - \frac1{n^2}$

大胆猜想，小心求证。

基础情况（ $n = 1$ ）： $\frac1{1^3} \le 2 - \frac1{1^2}$ 显然成立。

归纳假设：假设对于 $n = k,(k\ge 1)$ 有 $\sum_{i=1}^{k}\frac1{i^3}\le 2 - \frac1{k^2}$ 。

归纳步骤：下面证明 $n = k + 1$ 的情况。

$\sum_{i=1}^{k + 1} \frac1{i^3} = \sum_{i=1}^{k} \frac1{i^3} + \frac1{(k+1)^3} \le 2 - \frac1{k^2} + \frac1{(k+1)^3}$

$= 2 - \frac1{(k+1)^2} - \frac{k^2 + 3k + 1}{k^2(k+1)^3} \le 2 - \frac1{(k+1)^2}$

综上，根据归纳原理，更强的命题成立。

于是， $\forall n\in\mathbb{N}^{*}, \sum_{i=1}^{n} \frac1{i^3} \le 2 - \frac1{n^2} \le 2$ 。 $\square$

其实如果你还记得定理3.5的话，我们可以直接有：

$\forall n\in\mathbb{N}^{*}, \sum_{i=1}^{n} \frac1{i^3} \le \sum_{i=1}^{n} \frac1{i^2} \le 2 - \frac1{n} \le 2$

3.6.7 二进制数

求证每一个正整数 $n$ 都可以写成二进制。换句话说，我们可以写作

$n = c_k\cdot 2^k + c_{k-1}\cdot 2^{k-1} + ... + c_1\cdot 2^1 + c_0\cdot 2^0$

其中，$k\in\mathbb{N}\wedge c_i \in \{0,1\}, i = 0, 1, ..., k$ 。

解答

证明：对 $n$ 进行强归纳。

基础情况（ $n = 1$ ）：$n = 1 = 1\cdot 2^0$ 成立。

归纳假设：对于任意 $1 \le m \le n$，$m$ 都可以二进制表示。

归纳步骤：考虑 $n + 1$ 的情形，分两种情况：

1. 若 $n + 1$ 是偶数，由归纳假设，有

$\frac{n + 1}{2} = c_k\cdot 2^k + c_{k-1}\cdot 2^{k-1} + ... + c_1\cdot 2^1 + c_0\cdot 2^0$

$= \overline{c_kc_{k-1}...c_1c_0}, c_i\in\{0,1\}$

则

$n + 1 = 2\cdot\frac{n+1}{2} = 2(c_k\cdot 2^k + c_{k-1}\cdot 2^{k-1} + ... + c_1\cdot 2^1 + c_0\cdot 2^0)$

$= c_k\cdot 2^{k+1} + c_{k-1}\cdot 2^{k} + ... + c_1\cdot 2^2 + c_0\cdot 2^1 + 0\cdot 2^0$

$=\overline{c_kc_{k-1}...c_1c_00}, c_i\in\{0,1\}$

可以用二进制表示。 2. 若 $n + 1$ 是奇数，则 $n$ 是偶数，由归纳假设，有

$\frac{n}2 = c_k\cdot 2^k + c_{k-1}\cdot 2^{k-1} + ... + c_1\cdot 2^1 + c_0\cdot 2^0$

$= \overline{c_kc_{k-1}...c_1c_0}, c_i\in\{0,1\}$

则

$n + 1 = 2\cdot\frac{n}{2} + 1 = 2(c_k\cdot 2^k + c_{k-1}\cdot 2^{k-1} + ... + c_1\cdot 2^1 + c_0\cdot 2^0) + 1$

$= c_k\cdot 2^{k+1} + c_{k-1}\cdot 2^{k} + ... + c_1\cdot 2^2 + c_0\cdot 2^1 + 1\cdot 2^0$

$=\overline{c_kc_{k-1}...c_1c_01}, c_i\in\{0,1\}$

可以用二进制表示。

综上，根据归纳原理，原命题成立。 $\square$

3.7 作业题

3.7.1 斐波那契证明

令 $F_i$ 为第 $i$ 个斐波那契数，由 $F_{i+2} = F_{i+1} + F_i$ 且 $F_1 = 1, F_0 = 0$ 。求证：

$\sum_{i=0}^{n} F_i^2 = F_nF_{n+1}$

解答

证明：对 $n$ 进行归纳。

基础情况（ $n = 0$ ）： $F_0^2 = 0 = F_0F_1$ 显然成立。

归纳假设：假设对于 $n = k，k\ge 1$ 有 $\sum_{i=0}^{k} F_i^2 = F_kF_{k+1}$ 。

归纳步骤：则对于 $n = k + 1$ ，有

$\sum_{i=0}^{k + 1} F_i^2 = \sum_{i=0}^{k} F_i^2 + F_{k+1}^2 = F_kF_{k+1} + F_{k+1}^2$

$= F_{k+1}(F_k + F_{k+1}) = F_{k+1}F_{k+2}$

综上，由归纳原理，原命题成立。 $\square$

3.7.2 机场

假设我们有 $2n + 1$ 个机场，其中 $n$ 为正整数。任意两个机场之间的距离都不同。对于每个机场，恰有一个飞机从这个机场起飞并飞向最近的另一个机场。用归纳法证明存在一个机场，没有任何飞机飞向它。

解答

证明：对 $n$ 进行归纳。

其实下面的证明过程的思想当中还用到了极端原理，考虑最极端的情况往往对于我们考虑一般情况来说是一个好的起点。

基础情况（ $n = 1$ ）：考虑任意 $2\times 1 + 1 = 3$ 个机场 $A, B, C$ ，由于每两个机场之间的距离不同，所以一定有唯一的两个机场之间的距离是所有距离中最短的。不失一般性，设 $BC$ 的距离是最短的。于是，根据定义， $B$ 的飞机一定飞向 $C$ ， $C$ 的飞机一定飞向 $B$ ，从而没有任何飞机飞向 $A$ ，基础情况成立。

归纳假设：假设 $n = k$ 时，即有 $2k+1$ 个飞机场时，结论成立。

归纳步骤：考虑 $n = k + 1$ 时，一共有 $2n + 1 = 2k+3$ 个飞机场，和基础情况类似的，由于两两之间的距离各不相同，一定有唯一的两个飞机场之间的距离是所有距离中最短的，记为 $B, C$ ，根据定义，$B$ 的飞机一定飞向 $C$ ， $C$ 的飞机一定飞向 $B$。

考虑除了 $B,C$ 以外剩余的 $2k+1$ 个飞机场，根据归纳假设，在这 $2k+1$ 个飞机场中，存在一个飞机场 $A$ ，没有任何飞机飞向它。而 $B, C$ 处的飞机也不飞向 $A$ 。

因此，在所有的 $2k+3$ 个飞机场起飞的飞机中，没有任何飞机飞向 $A$。

综上，根据归纳原理，原命题成立。 $\square$

进度

恭喜完成离散数学与概率论第3讲《数学归纳法》所有内容的学习！